Relational Algebra : Introduction

• The relational algebra provides basic operations which can be performed over single or multiple relations in order to generate new relations(single or multiple). Relational algebra is a procedural query language which follows a particular syntax with the help of which, data can be accessed and retrieved very easily from single as well as multiple table/data sources.
• Certain operators are used to perform queries and retrieve desired results. These operators can perform certain operations on single attribute(called unary operator) or multiple attribute(called binary operator).
• There are six different types of operator that can be used to perform different operations. All of these are listed and explained below.

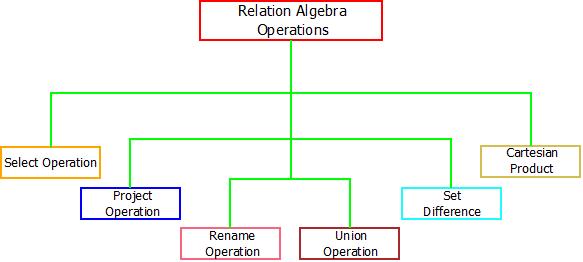
Relational Algebra : Operations

Relational Algebra : Operations

1. The Select Operation : This operation is used to fetch rows from given table or relation on the basis of given conditions, it is denoted by “Sigma(σ)”.

Syntax : σ <Condition> (Relation Name)

Here, “σ” is the select operation symbol. R is the relation from which the data needs to be fetched on the basis of conditions. Also, relational operators such as =, <, > etc. can also be used along. Let’s look at the example to get a clear picture of this.

For example : Consider the table of relation R(Roll No, Name, Age, Marks). If we want to select the name and age of student, then it can be done by:

Query Used : σ Name and Age>21 (Student_Details)

Relational Algebra : Select Operation

2. The Project Operation : This operation is also used to fetch all the rows/tuples/data according to the requested attribute. It means, using project operation one can simply fetch all the tuples corresponding to a single attribute or multiple attributes. It does not supports any conditions as select operation and is denoted using “Pie(π)”.

Syntax : π<attribute>(Relation Name)

For example : Consider the table of relation R(Roll No, Name, Age, Marks). If we want to project the marks column, then it can be done by :

Query Used : πMarks(Student_Details)

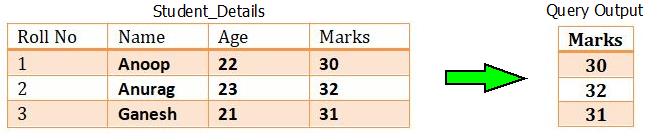
Relational Algebra : Project Operation

3. The Rename Operation : When operations like project and select are performed to fetch new results, these results requires renaming. They can be renamed using the rename operation which is denoted using Greek letter “Rho(ρ)”.

Syntax : ρ<New Name>(New Relation)

4. The Union Operation : In order to fetch data from two relations to generate new relation with combined capabilities, union operations can be used. The union operation fetches the data from both tables and projects it accordingly. It is denoted through “Union Symbol(U)”. Also, two things need to keep in mind while applying union operation are :

• Both the relations compulsory to have same number of attributes.
• Both the relations compulsory to have same domain for attributes.

Syntax : X1 U X2 , where X1 & X2 are two different relations satisfying the above two conditions.

For example : Consider the two tables with relations X1(Name, Age) and X2(Name, Age). If we wish to apply the union operation, then it can be done by :

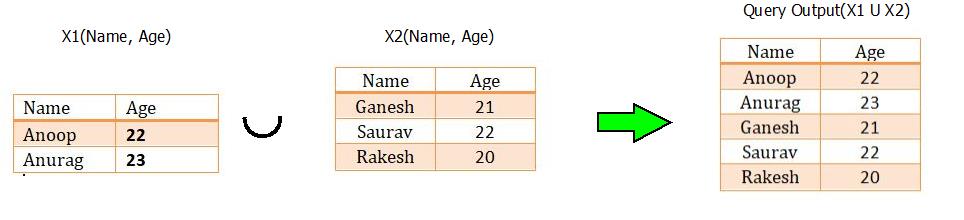
Relational Algebra : Union Operation 

5. The Set Difference Operations : In order to fetch the data which is not present in any one of the relation, set difference operation is used. The set difference operation is denoted by “Minus(-)”.

Syntax :  X1 - X2  or X2 - X1 , where X1 & X2 are two different relations having some attributes.

Note : X1 - X2  ≠ X2 - X1       {Not Commutative}

For example : Consider the two tables with relations X1(Name, Age) and X2(Name, Age). If we wish to apply the set difference operation, then it can be done by :

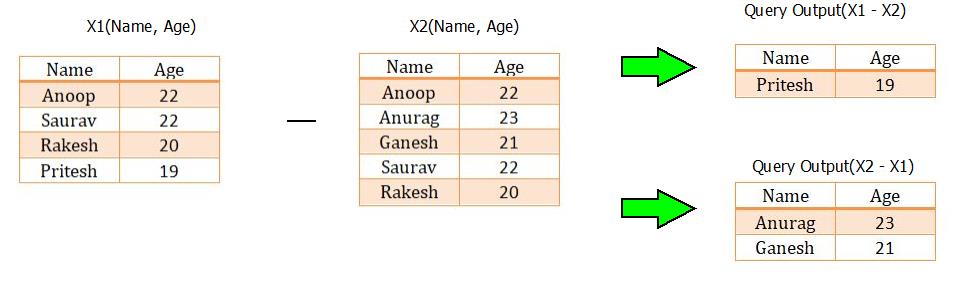
Relational Algebra : Set Difference Operation

6. Cartesian Product : The Cartesian product operation will generate the possible combinations among the tuples from the relations resulting in table containing all the data. It combines the information of two or more relations in one single relation. Cartesian product is different from union operation and is denoted by “Cross(X)”.

Syntax : A1 - A2 , where A1 & A2 are two different relations having some attributes.

For example : Consider the two tables with relations A1(Name, Roll No)and A2(Name, Roll No). If we wish to apply the Cartesian product operation, then it can be done by :

Relational Algebra : Cartesian Product Operation

Reference

Database Joins : Introduction

• Database joins are the alternate to the Cartesian product operation of the relational algebra concept.
• But, the logic behind the data set joins is same as that of a Cartesian product but, joins in database includes the option for condition which needs to be satisfied in order to get the desired results/output.
• The database joins has the ability of combining two or more data tables/tuples into a single table/table only if the following conditions are satisfied.
  • There must be a common attribute in both(tables which are participating) tables.
  • Join condition must be satisfied.
• Database joins can be broadly classified into two categories which are further categorized into sub categories. All of them are explained below.

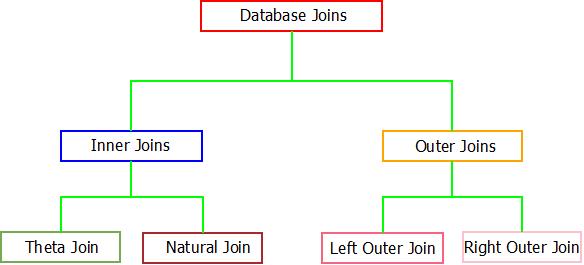
Database Joins : Classification

Database Joins : The Inner Joins

• The idea behind inner join is very simple. When inner join is applied to tuples or tables, only those tuples of the table are kept which have common attribute in all the tables. Other tuples which are not common are dropped from the resulting tuple/table.
• To implement this concept two possible inner joins are available i.e. Theta Join & Natural Join.

1. Theta Join

• If a condition is satisfied by the participating tables from different relations, then the tuples are combined together using Theta Join. Theta join is denoted through “Theta(Θ)”.

Syntax : R1(X1, X2,X3…Xn)  ⋈(Condition “θ”) R2(Y1, Y2,Y3…Yn) where, R1 and R2 are relations having (X1, X2,X3…Xn)  and (Y1, Y2,Y3…Yn) as attributes respectively.

For example : Consider the tables Student_Details and Student_Result. Now, if we want to implement theta join on these relations, the result will look like:

Database joins : Theta Join 

2. Natural Join

• Natural join does not supports any condition such as theta join and works only if, one attribute or more than one attributes are common between the joining/participating relations.

Syntax : R1(X1, X2,X3…Xn)  ⋈ R2(Y1, Y2,Y3…Yn) where, R1 and R2 are relations having (X1, X2,X3…Xn)  and (Y1, Y2,Y3…Yn) as attributes respectively.

For example : Consider the tables Student_Details and Student_Result. Now, if we want to implement natural join on these relations, the result will look like:

Database joins : Natural Join 

Database Joins : The Outer Joins

• Outer join overcomes the inability of inner joins of dropping the tuples which are uncommon among participating relations. If we want to display those tuples which are not common, the concept of outer join is used.
• Also, if all the tuples needs to be displayed from all the participating relations, outer joins can be used. They are of three types : Left Outer Join, Right Outer Join & Full Outer Join.

1. Left Outer Join

• There exists a concept of position(left or right) of relations in case of both left and right outer join.
• To implement left outer join, at least one entity needs to be common in the relations. All the attributes/tuples present in the left relation are recorded in the resulting relation along with those which are commonly present in the right relation.
• If in case any tuple in left relation does not matches with the tuple in right relation, NULL value will be displayed against that tuple in the resulting relation.

Syntax : R1(X1, X2,X3…Xn)   R2(Y1, Y2,Y3…Yn) where, R1(Left Relation) and R2(Right Relation) are relations having (X1, X2,X3…Xn)  and (Y1, Y2,Y3…Yn) as attributes respectively and "” denotes left outer join.

For example :  Consider the tables Student_Details and Student_Result. Now, if we want to implement left outer join on these relations, the result will look like:

DBMS Joins : Left Outer Join

2. Right Outer Join

• There exists a concept of position(left or right) of relations in case of both left and right outer join.
• The right outer join is completely similar to left outer join except the resulting relation will include all the tuples from relation present on right hand relation.
• Also, NULL value will be displayed against the tuple which doesn’t matches up with the left side relation.

Syntax : R1(X1, X2,X3…Xn)R2(Y1, Y2,Y3…Yn) where, R1(Left Relation) and R2(Right Relation) are relations having (X1, X2,X3…Xn)  and (Y1, Y2,Y3…Yn) as attributes respectively and "” denotes right outer join.

For example : Consider the tables Student_Details and Student_Result. Now, if we want to implement right outer join on these relations, the result will look like:

Database Joins : Right Outer Join

3. Full Outer Join

• In full outer join, both the relations are merged together which results in a relation consisting of all the tuples.
• If in case, tuples doesn’t matches, NULL value is passes against that.

Syntax : R1(X1, X2,X3…Xn)  R2(Y1, Y2,Y3…Yn) where, R1 and R2 are relations having (X1, X2,X3…Xn)  and (Y1, Y2,Y3…Yn) as attributes respectively and “ ” denotes full outer join.

For example : Consider the tables Student_Details and Student_Result. Now, if we want to implement full outer join on these relations, the result will look like:

Database Joins : Full Outer Join