Relational Algebra Operators

Relational Algebra-

 

Relational Algebra is a procedural query language which takes a relation as an input and generates a relation as an output.

 

Relational Algebra Operators-

  The operators in relational algebra are classified as-

 

 

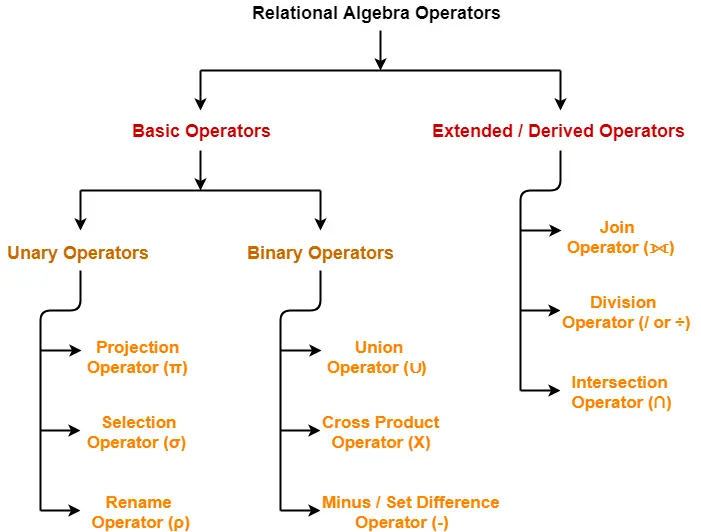
Characteristics-

 

Following are the important characteristics of relational operators-

• Relational Operators always work on one or more relational tables.
• Relational Operators always produce another relational table.
• The table produced by a relational operator has all the properties of a relational model.

 

Selection Operator-

 

• Selection Operator (σ) is a unary operator in relational algebra that performs a selection operation.
• It selects those rows or tuples from the relation that satisfies the selection condition.

 

Syntax-

 

σ<selection_condition>(R)

 

Examples-

 

• Select tuples from a relation “Books” where subject is “database”

σ_{subject = “database”} (Books)

• Select tuples from a relation “Books” where subject is “database” and price is “450”

σ_{subject = “database” ∧ price = “450”} (Books)

• Select tuples from a relation “Books” where subject is “database” and price is “450” or have a publication year after 2010

σ_{subject = “database” ∧ price = “450” ∨ year >”2010″} (Books)

 

Important Points-

 

Point-01:

 

• We may use logical operators like ∧ , ∨ , ! and relational operators like  = , ≠ , > , < , <= , >= with the selection condition.

 

Point-02:

 

• Selection operator only selects the required tuples according to the selection condition.
• It does not display the selected tuples.
• To display the selected tuples, projection operator is used.

 

Point-03:

 

• Selection operator always selects the entire tuple. It can not select a section or part of a tuple.

 

Point-04:

 

• Selection operator is commutative in nature i.e.

σ _{A ∧ B} (R) = σ _{B ∧ A} (R)

OR

σ _B (σ _A(R)) = σ _A (σ _B(R))

 

Point-05:

 

• Degree of the relation from a selection operation is same as degree of the input relation.

 

Point-06:

 

• The number of rows returned by a selection operation is obviously less than or equal to the number of rows in the original table.

Thus,

• Minimum Cardinality = 0
• Maximum Cardinality = |R|

Projection Operator-

 

• Projection Operator (π) is a unary operator in relational algebra that performs a projection operation.
• It displays the columns of a relation or table based on the specified attributes.

 

Syntax-

 

π<attribute list>(R)

 

Example-

 

Consider the following Student relation-

 

ID	Name	Subject	Age
100	Ashish	Maths	19
200	Rahul	Science	20
300	Naina	Physics	20
400	Sameer	Chemistry	21

Student

Then, we have-

 

Result for Query π_{Name, Age}(Student)-

 

Name	Age
Ashish	19
Rahul	20
Naina	20
Sameer	21

 

Result for Query π_{ID , Name}(Student)-

 

ID	Name
100	Ashish
200	Rahul
300	Naina
400	Sameer

 

Important Points-

 

Point-01:

 

• The degree of output relation (number of columns present) is equal to the number of attributes mentioned in the attribute list.

 

Point-02:

 

• Projection operator automatically removes all the duplicates while projecting the output relation.
• So, cardinality of the original relation and output relation may or may not be same.
• If there are no duplicates in the original relation, then the cardinality will remain same otherwise it will surely reduce.

 

Point-03:

 

• If attribute list is a super key on relation R, then we will always get the same number of tuples in the output relation.
• This is because then there will be no duplicates to filter.

 

Point-04:

 

• Projection operator does not obey commutative property i.e.

π _<list2> (π _<list1> (R)) ≠ π _<list1> (π _<list2> (R))

 

Point-05:

 

• Following expressions are equivalent because both finally projects columns of list-1

π _<list1> (π _<list2> (R)) = π _<list1> (R)

 

Point-06:

 

• Selection Operator performs horizontal partitioning of the relation.
• Projection operator performs vertical partitioning of the relation.

 

Point-07:

 

• There is only one difference between projection operator of relational algebra and SELECT operation of SQL.
• Projection operator does not allow duplicates while SELECT operation allows duplicates.
• To avoid duplicates in SQL, we use “distinct” keyword and write SELECT distinct.
• Thus, projection operator of relational algebra is equivalent to SELECT operation of SQL.

Set Theory Operators-

 

Following operators are called as set theory operators-

 

 

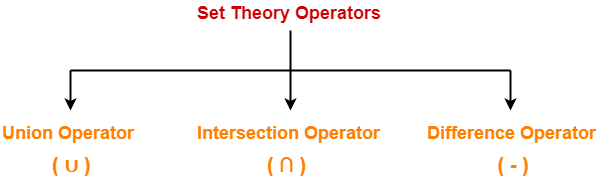
1. Union Operator (∪)
2. Intersection Operator (∩)
3. Difference Operator (-)

 

Condition For Using Set Theory Operators   To use set theory operators on two relations, The two relations must be union compatible. Union compatible property means- Both the relations must have same number of attributes. The attribute domains (types of values accepted by attributes) of both the relations must be compatible.

 

Also read- Selection Operator and Projection Operator

 

1. Union Operator (∪)-

 

Let R and S be two relations.

Then-

• R ∪ S is the set of all tuples belonging to either R or S or both.
• In R ∪ S, duplicates are automatically removed.
• Union operation is both commutative and associative.

 

Example-

 

Consider the following two relations R and S-

 

ID	Name	Subject
100	Ankit	English
200	Pooja	Maths
300	Komal	Science

Relation R

 

ID	Name	Subject
100	Ankit	English
400	Kajol	French

Relation S

 

Then, R ∪ S is-

ID	Name	Subject
100	Ankit	English
200	Pooja	Maths
300	Komal	Science
400	Kajol	French

Relation R ∪ S

 

2. Intersection Operator (∩)-

 

Let R and S be two relations.

Then-

• R ∩ S is the set of all tuples belonging to both R and S.
• In R ∩ S, duplicates are automatically removed.
• Intersection operation is both commutative and associative.

 

Example-

 

Consider the following two relations R and S-

 

ID	Name	Subject
100	Ankit	English
200	Pooja	Maths
300	Komal	Science

Relation R

 

ID	Name	Subject
100	Ankit	English
400	Kajol	French

Relation S

 

Then, R ∩ S is-

 

ID	Name	Subject
100	Ankit	English

Relation R ∩ S

 

3. Difference Operator (-)-

 

Let R and S be two relations.

Then-

• R – S is the set of all tuples belonging to R and not to S.
• In R – S, duplicates are automatically removed.
• Difference operation is associative but not commutative.

 

Example-

 

Consider the following two relations R and S-

 

ID	Name	Subject
100	Ankit	English
200	Pooja	Maths
300	Komal	Science

Relation R

 

ID	Name	Subject
100	Ankit	English
400	Kajol	French

Relation S

 

Then, R – S is-

 

ID	Name	Subject
200	Pooja	Maths
300	Komal	Science

Relation R – S

..